Quantum Physics and Quantum Technology

Biography

Biography: Eliade Stefanescu

Abstract

A system of fermions is usually described by a Hamiltonian with Fermionic operators. However, such a system is never isolated, but in a dissipative environment of the free electromagnetic field at a certain temperature, of the collective rotations and vibrations of this system, or of the support system, and of other neighboring particles. The dissipative dynamics is usually described as a time-dependent dynamic semigroup, depending on unspecified, phenomenological parameters. In this framework, more or less at the same time with other authors, we found that dissipation increases the penetrability of a potential barrier, fitted a cold fission spectrum, and calculated the width ratio of the two bumps of a double nuclear giant resonance. However, in the following investigations, we used the more physical method of Ford, Lewis, and O’Connell, providing explicit, microscopic coefficients. In this way, we derived master equations for Fermions, Bosons, and electromagnetic field, imagined a device converting environmental heat into usable energy, and effectively calculated the physical characteristics of such a device. This description is based on two different theories: quantum mechanics, and the electromagnetic theory. Here we show that the equations of these two theories can be obtained in the same theoretical framework, of a unitary relativistic quantum theory. We conceive a particle as an unconventional wave packet in the coordinate and momentum spaces, providing the two Hamilton equations as group velocities in these spaces, while the Hamiltonian in the time dependent phase of the conventional wave packet is replaced by the Lagrangian. We adopt a relativistic quantum principle, asserting that the time dependent phase is invariant to an arbitrary change of coordinates. When a finite spectrum is considered, the relativistic dynamics is obtained for a quantum particle. We describe the interaction of such a particle with a field by a variation of the time dependent phase, with terms proportional to the coordinate and time variations, while the coefficients of these terms define the vector and scalar potentials of this field. From the group velocities of a quantum particle, we obtain the Lagrange equation, the Lorentz form of a mechanical force, and three Maxwell equations. For a field propagating with the limit velocity c of the quantum particle waves, the fourth equation, Ampère-Maxwell, is obtained. In this theoretical framework, we obtain the spin as a characteristic of a quantum particle, and demonstrate the spin-statistics relation.

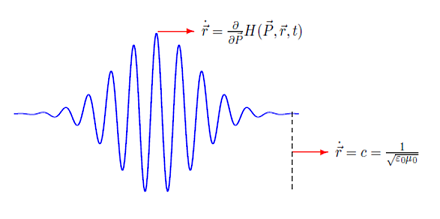
Figure: Quantum particle wave-packet with a limit velocity c, interacting with

an electromagnetic field propagating with this velocity.

Recent Publications:

[1] Sargsyan, VV, Kanokov, Z, Adamian, GG, Antonenko, NV (2016), Application of the Theory of Open Quantum Systems to Nuclear Physics Problems, Physics of Particles and Nuclei, vol. 47, p. 157. 

[2]  Stefanescu, E, Sandulescu, A & Greiner, W (1993), Quantum tunneling in open systems, International Journal of Modern Physics E, vol. 2, p. 233.

[3]  Stefanescu, E, Scheid, W, Sandulescu, A, & Greiner, W (1996), Cold fission as cluster decay with dissipation, Physical Review C, vol. 53, p. 3014.

[4]  Stefanescu, E, Liotta, RJ & Sandulescu, A (1998), Giant resonances as collective states with dissipative coupling, Physical Review C, vol. 57, p. 798.

[5]  Ford, GW, Lewis, JT & O’Connell, RF (1996), Master Equation for an Oscillator Coupled to the Electromagnetic Field, Annals of Physics, vol. 252, p. 362.    

[6]  Stefanescu, E (2010), Master equation and conversion of environmental heat into coherent electromagnetic energy, Progress in Quantum Electronics, vol. 34, p. 349.

[7]  Stefanescu, E (2014, vol. 2 in print), Open Quantum Physics and Environmental Heat Conversion into Usable Energy, Bentham Science Publishers, Sharjah (UAE), Brussels, Danvers (Massachusetts, USA).

[8]  Stefanescu, E (2014), The relativistic dynamics as a quantum effect, Journal of Basic and Applied Research International, vol. 1, p. 13.