
Biography
Biography: Adam Baskerville
Abstract
Electronically excited states are vital for the analysis of spectroscopic properties. However, usually theoretical methods assume that nuclei are infinitely heavy. Recently we have shown that it is possible to calculate high accuracy, non-relativistic excited S state energies and wavefunctions for three particle systems using a series solution methodology. In this talk, details of the theory and implementation will be described and the latest results presented. This builds upon our previous work for the ground state problem which uses a series solution method utilising a triple orthogonal Laguerre polynomial wavefunction to investigate the bound state properties of the ground state of three-particle atoms and molecules. The excited state implementation is based on the work of Pekeris, however in the present work the effects of nuclear motion are explicitly included. It is found, contrary to the matrices for the ground state problem, that the matrices become denser in the excited state formulism. Up to three non-linear variational parameters can be used to improve the rate of convergence, and the quality of the wavefunctions is assessed using various exact conditions and identities.
The content in this talk highlights the versatility of using the series solution method to solve a non-separable Schrodinger equation, and how a Laguerre-based wavefunction captures the physics of excited states. Furthermore, this method could potentially be used to probe highly excited Rydberg states which have recently been proposed as a possible logic gate in quantum computing applications.
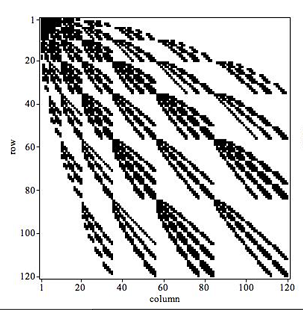
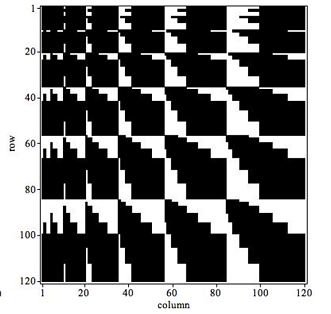
Figure: Comparison of the secular equation for the ground state problem (left) vs. the excited state problem (right). White = zero elements, black = non-zero elements.

